Do you remember when you learned how to count numbers for the first time? you learned to count (1, 2, 3, … , 9 then 10) and maybe later on you learned the number 0. This is called decimal numbers where we use 0, 1, 2, … 9 in a digit. Numbers have digits of ones, tens, hundreds and so on. Each of these digits can take only numbers from 0 to 9 (ten numbers) only. If we want to express numbers larger than 9 we use the next digit and start counting again.
I am not here to teach you how to count but it will make explaining today’s topic easier. What if I tell that there are other numbering systems out there! In computers and programming world binary numbers and hexadecimal numbers are used so much, if you are into programming you have to learn these.
That’s what I want to talk about today.
Binary Numbers
Now imagine that instead of 0, 1, 2, …,9 we only have 0 and 1. Lets count with only 0 and 1, (0, 1, 10, 11, 100, …). This is how to count in world where digits use only 0 and 1, when you reach 1 you go to the next digit (see table 1 below to compare decimal with binary). This type of number called binary numbers.
Why is this used? Well computers only understand 0 and 1 despite what you see on screen. These 0 and 1 are actually a representation of the electric voltage state in the circuitry inside the computer. 0 for LOW voltage or 0 volts, while 1 is HIGH or 5 volts or 3.3 volts and sometimes less. Also when data is sent from machine to machine they are sent through zeros and ones which means a series of signals of LOW and HIGH voltages are sent (there are other ways to transmit data but that’s for another topic). DRAMs save data by charging millions of internal capacitors with LOWs or HIGHs and that translated to 0s and 1s.
I like these type of examples because they show how binary is related to the physical world and not some software world created by humans. I also saw that binary is used in application not directly related to physical world as the examples above like IP addressed and subnetting in networking.
You can also see from above that understanding binary helps learn how computers work and operate, it all comes down to 0 and 1, LOW and HIGH, ON and OFF, 0 volts and 5 volts, TRUE and FALSE, + and -, or any other way to refer to binary.
| Decimal number | Binary number | Hexadecimal number |
| 0 | 0b0 | 0x0 |
| 1 | 0b1 | 0x1 |
| 2 | 0b10 | 0x2 |
| 3 | 0b11 | 0x3 |
| 4 | 0b100 | 0x4 |
| 5 | 0b101 | 0x5 |
| 6 | 0b110 | 0x6 |
| 7 | 0b111 | 0x7 |
| 8 | 0b1000 | 0x8 |
| 9 | 0b1001 | 0x9 |
| 10 | 0b1010 | 0xA |
| 11 | 0b1011 | 0xB |
| 12 | 0b1100 | 0xC |
| 13 | 0b1101 | 0xD |
| 14 | 0b1110 | 0xE |
| 15 | 0b1111 | 0xF |
Prefixes 0b and 0x are used for binary and hex numbers respectively in C language
Hexadecimal Numbers
After talking extensively about binary, understanding hexadecimal numbers will be easy (or hex numbers).
Now for hex numbers the numbers in a digit are 0, 1 , 2, …, 9, A, B, C, D, E and F. these are 15 numbers. Lets count to 18 in hex (0, 1, 2, …, 9, A, B, …, F, 10, 11, 12) where 10 in hex equals 16, 11 in hex equals 17 and 12 in hex equals 18. Refer to table 1 above to see numbers from 0 to 16 in hex.
Why we use this? If you deal with computers, they mainly use binary. However, this is difficult for humans to read for example for 32 bit ARM microcontrollers, registers are 32 bit wide, what if the value there was 1111 1110 1101 1100 1011 1010 1001 1000 !!!! this is how 32 bits look like.
Now in order to make this human readable hex numbers are used. You can combine 4 binary digits into one hex digit. The above number can be converted to hex FEDC BA98.
When we program microcontrollers although we are really dealing with binary numbers, but when writing programs we use hex numbers. Sometimes we want to program one byte of data, so we can control 8 binary bits with just 2 hex numbers. In other words, in reality we control pins (turn them on or off for example) in binary, but when programming a bunch of pins (a full byte for example) we use hex numbers to make it easier and more readable.
Decimal, Binary, Hexadecimal conversion
There is a manual way to convert between these types and you can search online or study it. This is out of this articles scope I just wanted to introduce these numbering systems.
Memorizing the table above is a good start. Also if you use windows you can use the built in calculator to convert between binary and decimal and hex very easily as shown below (the 32 bit number above can be seen in the picture).
Choose Programmer from settings
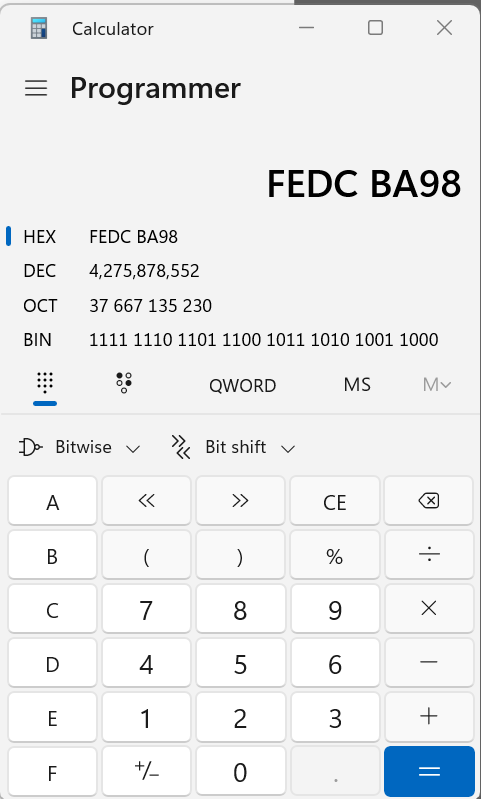
Enjoy converting




